An honest take on options
Why I love them, some thoughts on option modelling, real example of a trade and what to expect if you are just starting
This HOTF article will be focused on a derivative we love to use - options. I am unsure of how well versed our audience is in this realm, so let’s begin with the basics. An option gives its owner the right but not the obligation to buy or sell the underlying (the asset of which the option is a derivative) at any given moment (will keep the example with US expiration options as this is what we actually trade most of the time) before the option’s expiration at a given price, which is called strike.
You can hardly avoid stumbling upon a read about the basics on options during your trading journey, but if you have, I think tasty trade is a neat place to start (no affiliation). You can find plenty of Options 101 information there, the usual option structures such as spreads, flies, etc. and some advanced concepts. This write up is not meant to go through every detail. On the contrary, it is just a take on why I think they are a must have in a trader’s toolkit. So, let’s cut to the chase and not waste time.
Why I love options
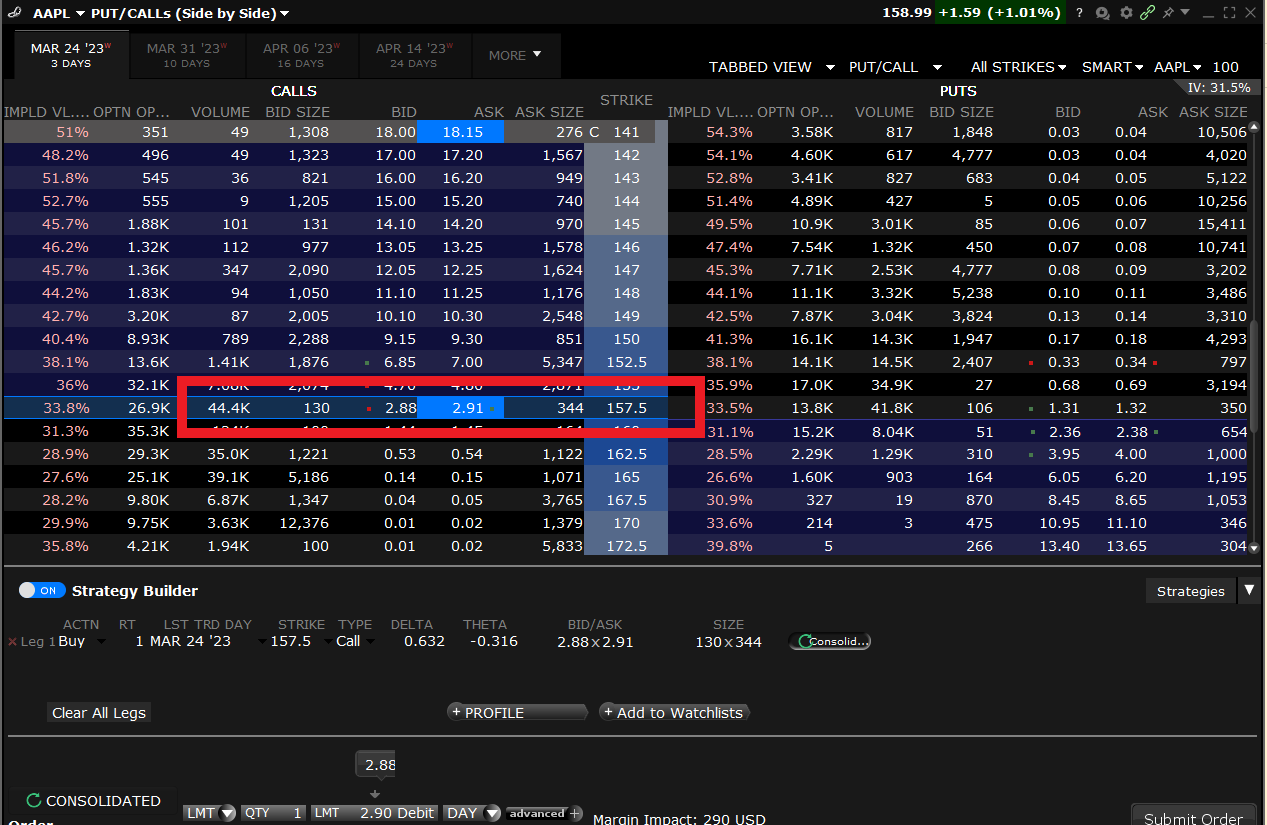
Know how much you risk - if you buy an option (or a spread and other structures too, but let’s limit ourselves to spreads/calls/puts), the total amount you can lose is the premium you pay for it. Let’s look at the option chain (where options are displayed on a broker’s platform) of everyone’s favourite stock - AAPL.
The option to buy 100 shares (i.e. call option) of AAPL at 157.5$ (strike) right now will cost me 2.91$ if I lift the ask. As 1 option contract is standardized to give you 100 shares of the underlying stock, the total amount you risk (can lose) by buying the option will be 2.91$x100 or 291$. It does not really matter whether the stock will gap down, what will happen with the banks or what Powell will say. The maximum amount you can lose is 291$. This is wonderful but note that you do pay for this feature as the stock is trading at 158.9$, not at 160.41$ (157.5$+2.91$). The difference of 1.51$ is what you call extrinsic value, or the part of the option that is not already captures within the price of the underlying.
Leverage - buying power is rarely an issue - as mentioned above, the AAPL call option will give you the right to buy 100 shares by only putting 291$ to work. This is why retail guys love options. You do not need your account to be big in order to play large cap equities in size. It does not require you heavy math skills to see that for 291$ you are ”in control” of 100x 157.5$ = 15 750$ worth of the underlying stock. And not only this, but the collateral/margin you have to put down to be able to be “in control” of that notional value is merely the premium paid (291$).
Liquidity - some options are liquid, others are not. And some have big spreads which do not always fill you at the mid (right between the bid and ask prices), which is considered the fair value. But if you need to get a big position ASAP for a momentum play and there is a risk of not being filled with the underlying, I can assure you that the depth of the option book will get you faster to the desired notional value of the position than the depth of the book of the underlying. Lately, I have been surprised how thinly traded some of the S&P 500 stocks are.
Game on a game - this one is my favourite. Options often make you feel like you are playing a meta version of the stock market. There is so much going on and the creativity that you can experience in terms of how to express your idea is unmatchable. Let’s say you do not want to participate in AAPL at this price as it just broke resistance near 155$ and you fear being shaken out. But you also see a chance of it shooting higher today on a positive reaction to what Powell says, creating a parabolic movement. You could go further out on the call strikes (called out of the money options or simply OTM) and buy a call spread (buy 162.5$ and sell 165$) for 40c. This would allow you to twist the risk - reward of the play (lose 40c, gain 2.1$ max) significantly in a favourable way, by betting on something that the market has decided to have a lower probability than what you think it has (AAPL is used for exemplary purposes only). And it does not stop here, you can make combinations of stocks and options, make ratio spreads or butterflies .It all depends on how YOU think your idea is about to materialize and whether the market has underappreciated your view.
Allows you to bet on volatility and time - there is no way to discuss options without mentioning two of the option’s price crucial components - the volatility of the underlying and the time to expiration of the option contract. There is a positive but non-linear (i.e. non-constant) relationship between the price of an option and the volatility of the underlying asset. It makes sense that higher volatility increases the chances of OTM calls and puts to end up being in the money. Similarly, there is a negative and but non-linear relationship between the option price and the time left until the option expires. A deep understanding of these and other components which end up modelling the price of the option is immensely valuable and not only allows one to bet on volatility and time but forces the user to take those into consideration.
Why I believe it is appropriate to trade options
To finish off the helicopter view on options and talk through why I believe options are the asset to go to now, I have to briefly get more technical. But bear with me as I will try to continue using plain English and stay away from any calculations.
Here is the classic Black-Scholes Model used to price options:
Messy, is it not? The nice part is no one around me uses it. We take the option price we see on the option chain as the right and fair outcome of this or a more sophisticated new version of the Black-Scholes model. However, I do know the components and how they affect the price (+ or - or linear / non-linear relationships). As written above, volatility plays a huge positive role in the price of an option. But how do you know the volatility that is about to come in order to price the option correctly? Well, you do not and here is the sexy part. Option models use realized volatility as a proxy for future volatility and put a mark up on it as a safe margin (also called variance RISK premium; quite in contrast to what I had just phrased it) which tends to be what compensates the part taking the other side of your bought call/put. This is an important take away - option prices are based on what has happened plus something on top.
On a separate note, the complex world of science (and finance) cannot be distilled into a model but people need models to understand the world. That’s how our brains operate. In order to get from a very complex non-modelable (just invented this word) topic to a modelable, one goes through A LOT of non-real life assumptions. In the case of Black Scholes, they are the following according to investopedia.com:
Ridiculous or not, those were needed in order to come up with a price of an option back then. Most of those are fixed or amended through time in order to fit the real world much better, but as no one has managed to ‘figure out’ the market. Thus, we still believe the one that says “The returns of the underlying asset are normally distributed”. And it is true MOST of the time. The “normally distributed” returns are displayed as the so call bell-curve where the average sits in the middle and the deviations (in statistical language - st. dev.) are away from it both left and right. According to it, within 99.9% of the time, the markets’ returns should not be more than 3 st. dev. away from the average.
But how come we hear about 5-6 st. deviation moves every year when basically no one should have observed those? There is an article about st. deviation moves of S&P 500 if you want to delve more in it here. The most recent developments in the Eurodollar market for sure were not to be seen according to the normal distribution but I cannot pin point how many st. dev. the move was. Not that it matters. What matters is, stuff happens every now and then (more often than predicted) and catches the models off-guard in a big way. And every day, there are tiny corners of the markets where it happens in a small way. Where you believe the price displayed does not fully capture what is about to unfold. Such events are short squeezes, parabolic moves, non-priced catalysts, etc.
I cannot prove it mathematically as I am as good as an average Joe is at it, but the simple logic is this - once you shake the assumptions of the model (which happens when the market hits turbulence), it does not work too well. And if it does not work too well it means most probably the prices it gives are not as fair as those it gives when there is no turbulence. And the harder the turbulence, the larger the relative ”unfairness”.
This does not mean once the turbulence (which is usually volatility) hits hard you go out and buy simple calls which have ballooned in price. No, it means that you go out looking for option structures that are MORE likely to happen than what you feel is predicted by price or AT LEAST will likely give you a chance to get out during the ups and downs that come with the volatility.
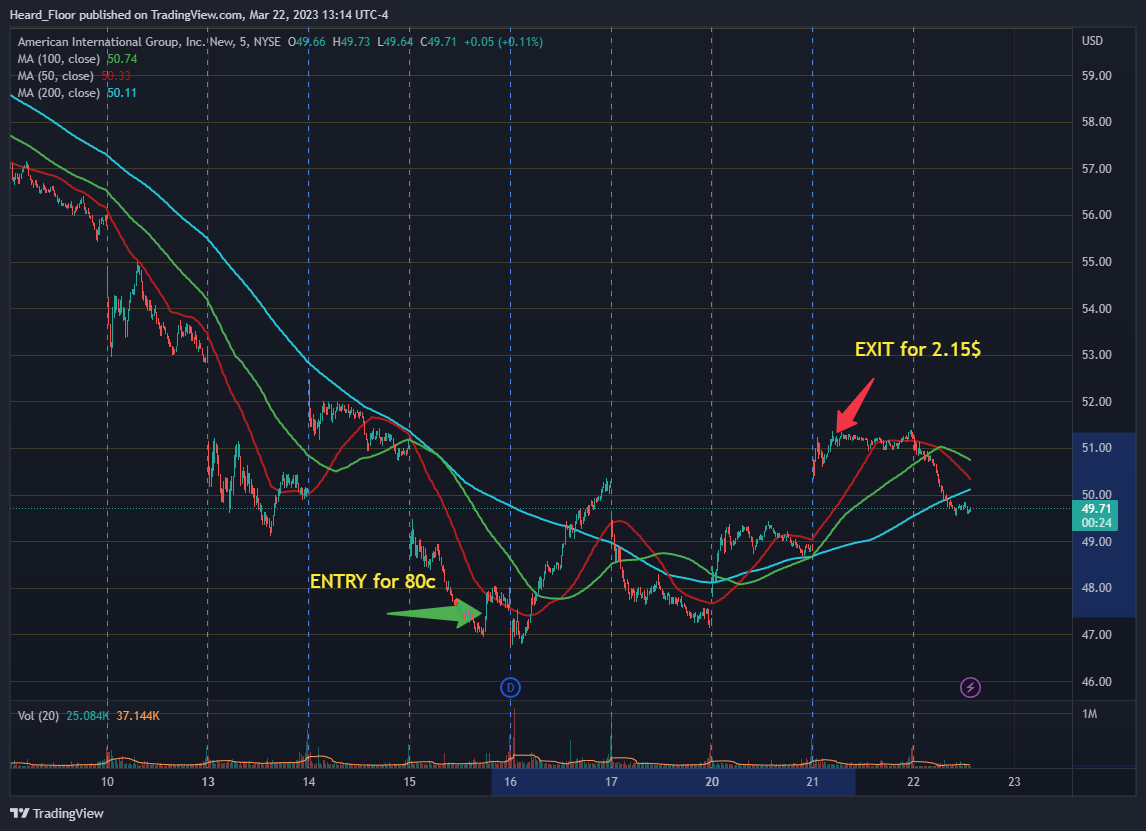
A real life example of this would be a trade I did recently and commented on in the last weekly review - a call spread 49$-53$ call spread in AIG expiring Mar 24. Make no mistake, I was extremely selective and wanted to bet on a bounce from much oversold conditions which met AIG on well-formed prior support level. I also had a fundamental angle that insurance stocks are sold in a sympathy way to banks. What is more, on the technical side, I knew the yo-yo has stretched and the odds of it bouncing to the above were in my favour.
Buying a 4$ spread for 80c seemed like a good deal, despite the upper strike being more than 10% away to the above. And that was a bet through ex-div day, meaning the dividend was discounted from the price (not included in the ‘basic’ Black Scholes model but included in what we see on the screens every day). Best part of the trade was that I had limited risk in the most uncertain time. This allowed me act at a moment, price and level where the phrase ‘catching the knife’ would vastly underestimate the situation. And I also had the luxury of giving it a bit more than a week for the market to find its ground. To be honest, I had a similar trade with MET that did not work out too well (bought for 1$, sold for 1.4$) and one in XLF where I got rather early and exited for a 3/4 loss of the total premium. After all, you cannot catch them all. What is important is to be net positive.
Why trading options is hard and what to expect when you start trading
This piece was not intended to throw people who do not know what an option is straight into a trading frenzy. It was intended to show what I like about them - mainly the limited risk and the creativity they allow me to have. But none of these comes free. If one is not selective, i.e. bets not when he believes his expectations are not reflected well in the price, he/she will play a negative expectancy value game. And here comes the first and most important reason why options are hard - they require you to have your inner clock working right so you can spot these so called value bets. Options are not the idea itself, just a tool to realize an idea on the underlying that you already have. And learning how to spot value bets takes a lot of time.
For those who are just starting, I have bad news. If you are like me, expect to spend a substantial amount of time trying out what is what until you understand how the different components of an option fit together (greeks, strike, underlying). It is not uncommon for an option to lose money even if you guess the directions correctly. There is plenty of other things that could screw you. This is why trading options is much harder than trading the underlying. As it is common in our business, learning costs you both time and money.
Good luck to those who are yet to start trading options. Feel free to reach out for help.
Some sources that I believe are very helpful and must reads before you spend real money trying to figure this out:
Options, Futures, and Other Derivatives by John C Hull
Brent’s blog has some very nice free articles about options